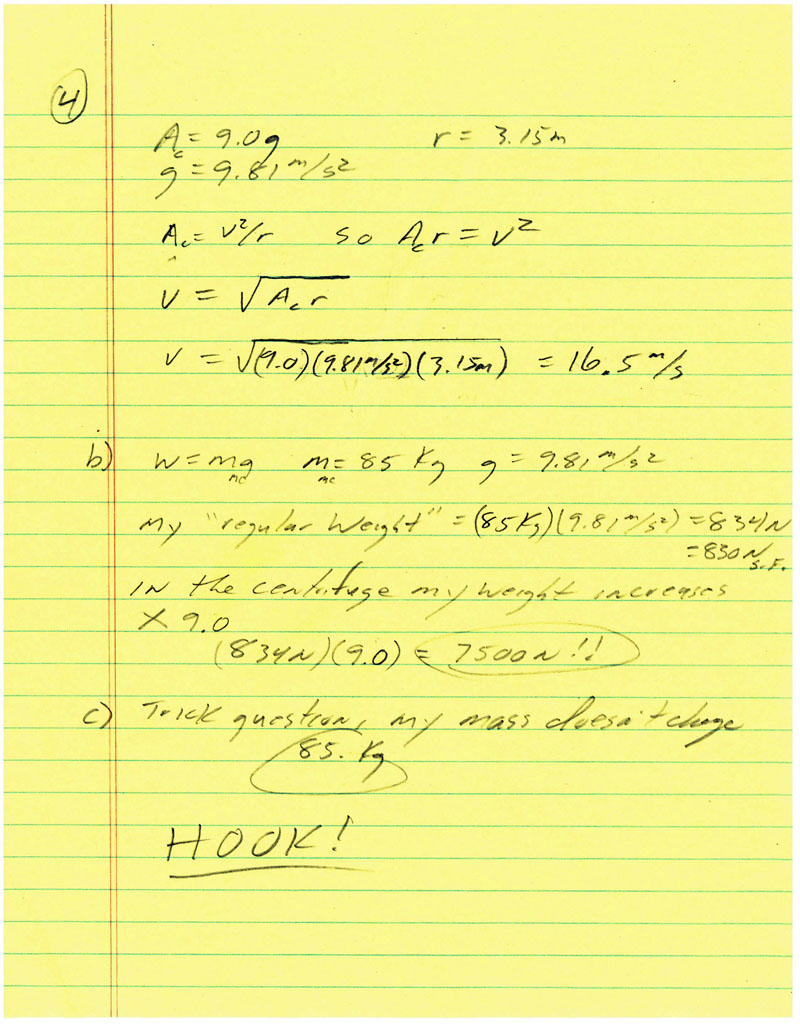1) Let's saythat you are orbiting the earth at an altitude of 6.371 x 106 meters above the surface of the earth.
a) Calculate the velocity at which you are orbiting the Earth at that altitude.
b) Why is it that I would orbit the Earth at that exact velocity?
c) Why would a 9,000,000. kg chunk of rock "orbit" at exactly that same velocity?
d) What did you learn from this exercise?
2) Measure the height of your chair.... *precisely*.
Stand on top of your chair.
Jump off of your chair.
Calculate the force between you and the Earth just the tiniest fraction of a second after you stepped off your chair.
Calculate your acceleration towards the Earth using the force you calculated above and Newton's 2nd Law.
Calculate the acceleration the Earth experienced at that same time.
- What did you learn from this exercise?
NOTE: The extra .50 (or so) meter you are above the center of the Earth is so small a difference (compared to the diameter of the Earth) as to be irrelevant!
3) A typical lightweight helicopter blade (mass = 100. kg) rotates at about 450 revolutions per minute. How fast is that in revolutions per second?
a) What is the circumference of the circle swept out by that blade?
b) If the rotor blade is 5.50 meters in diameter, how much force does the blade experience at the outside tip?
4) Fighter pilots typically black out when they experience an acceleration of about 9.0 times the acceleration due to gravity. How fast must the training "centrifuge" (radius 3.15 meters) spin (in meters per second) in order to generate that level of acceleration?
b) How much would your weight change at that time?
c) What would your mass be?
By the by, fight pilots often say (or grunt) the word "HOOK!" during such times... why is that? Try it!
NOTE: Pilots say, yell or grunt the word "HOOK!" when conducting high "g" maneuvers because that's an easy way to forcefully constrict your core muscles which helps drive blood back to their extremities!
6) The planet Mars and the Planet Earth both orbit the Sun. They do not, however, orbit each other.
What is the largest gravitational force experienced between those two planets?
When does that occur?
When is the least gravitational force experienced between those two planets?
Calculate the force between Earth and Mars at that time.
b) There is another much stronger gravitational force experienced by both planets at that particular time...what force might that be?
Calculate that force: