
BACKGROUND: Review this image from the book example:
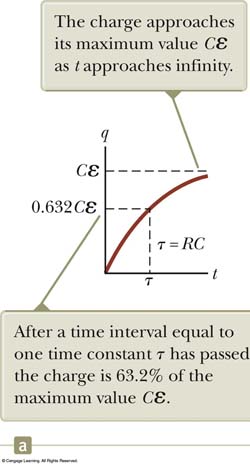
Notice how the charge changes as the capacitor is charging when switch is at "a" (You'll need these to establish your limits of integration)
Similarly for a discharging capacitor when the switch is at "b":
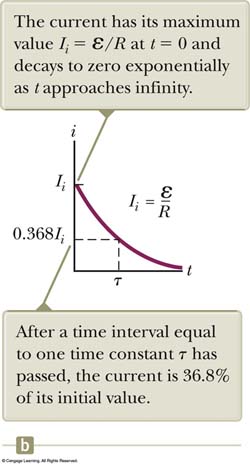
NOTE: The time constant τ has no relevance in this take home
════════════════════
You have a 15 point take home test.
LET'S PRETEND we are generating a first time solution to a wonderful differential equation and we'll be publishing that in a prestigious physics journal. That means all our work will be standing tall, fully and completely annotated and looking pretty when it is turned in next Monday. If you miss the publication submittal date, your work will NOT be evaluated (Seriously!)
Because this exquisite paper is being considered for publication, you'll make extra-special double scoop efforts to ensure that your exquisite paper is fully annotated, meticulously formatted, free of scratch marks (by hand if you please) and otherwise looking pretty and standing tall by next Monday @ 0100 Zulu Time (at the Grenwich Observatory on the Grand Meridian-- that would be 13:00 hrs on the 25th day of March in the year two-thousand and nineteen of the Western Calendar (as ammended by Gaius Julius Caesar and Pope Greggory XIII)
════════════════════
But I Digress...
The book shows most of an outline of the math required to create and solve a differential equation relating to the charging/discharging of a capacitor over time.
PART I (10 Points)
Your tasque is to do a much more thorough job in creating a fully annotated solution begining with the voltage-drop equation for a basic RC circuit:
(Initial EMF voltage) - (voltage drop through the capacitor) - (voltage drop through the resistor) = 0
Which we can (and WILL!) write mathematically as:
ε - Q/C - IR = 0
Following the steps shown beginning on page 847, you will create an articulate, accurate, and most especially fully annotated STEP - BY - STEP elegant solution to the problem.
The reason I'm insisting that you not omit any single step, is that the author skips huge swaths of steps, and there is very definitely devil lost in the detail.
To wit, you are NOT allowed to skip a single step... if you move one term from one side of the equation to the other you must list that and annotate it. You must NOT combine any steps (If I let you combine two steps, then perhaps you'll combine 3 or 4 or 5 steps and then we're right back to where we started from. This is non-negotiable so please don't ask.
Also, each annotation should be clear and accurate... no cryptic phrasing. When in doubt write in full word sentences.
Your solution MUST precisely match the final equation in the book. It's not good enough for your solution to provide the same results... this is a famous equation in physics, and we are trying to derive it precisely.
════════════════════
REGARDING LATE WORK & EXCUSES
I won't entertain ANY conversations that begin with, end with or include any phrasing containing, alluding to or in anyway relating to the following:
"BUT MR W THAT STEP IS SO OBVIOUS, I SHOULDN'T HAVE TO ANNOTATE THAT ONE"
The only thing you have to lose in annotating everything is a few moments of your time.
You will also be graded on neatness, completeness and readability. Remember, we are going to pretend this is being submitted for publication (I DO encourage you to have some fun with that.... perhaps a cover letter or some such?)
Just FYI, my solution on this part goes to 5 pages.
════════════════════
PART II (5 points)
The second part of the exam is to do the exact same thing for a discharging capacitor (that's a whole lot easier-- my solution is 1 1/2 pages). The books' rather abbreviated solution is described in "Discharging a Capacitor" on page 849.
Your solution MUST precisely match the final equation in the book. It's not good enough for your solution to provide the same results... this is a famous equation in physics, and we are trying to derive it precisely.
════════════════════
This may seem kinda easy.... perhaps it will be, but most likely it won't. I won't accept any excuses whatsoever for late work including but not limited to the following:
-
I got nothin' <sorry>
-
A meteor crashed into my house and ALL my exquisite notes caught fire.
-
My cat, dog, canary, mongoose (or other household pet) ate, crapped on, peed on, barfed on or otherwise did away with my exquisite notes
-
Mr W I didn't know it would be so hard... I'm really (and truly) sorry
-
I had to study for <fill in the blank other class>
-
My mom, dad, aunt, uncle, 2nd cousin-once removed etc ad nauseam was in an unfortunate accident with a (allosaurus, crocodile, city bus, solar flare, sewage treatment plant explosion, tricycle traveling at mach .75, thunderbolt, tornado, Cascadia Subduction Zone upheaval, Puget Sound Tsunamis, a hail storm with softball hail stones that fall and burn on the ground, plagues of freshmen zombies etc ad nauseam)
-
You contract beriberi, Dengue Fever AND the Plague on a quick jaunt out of town to Equatorial Guinea....
- Your least gracious and least humble instructor quits to seek spiritual enlightenment in Bhutan (they have a Gross National Happiness Index there, it's true!)... which is to say, the project is due EVEN IF I'M NOT HERE!
My very ungracious and certainly not-at-all humble response will be, I'm sorry to say:
"I DON'T CARE"
<sorry in advance>
Which translate into an "F" in the gradebook <ouch!>
════════════════════
Hmmmm, so you are freaked out and you cut class to avoid turning in the assignment, how do you suspect that will go?
════════════════════
You have one week from today. Your exquisite paper, standing tall and looking pretty are due at the beginning of class next Monday.
In case you didn't notice, I'm doing my best to FORCE you out of your usual "wait until the last minute" mode. There is a very good chance this will take a whole lot longer than you think it will.
Now... how shall we deal with *ahem* collaboration? My thoughts are to allow you to collaborate under the following conditions:
- You FIRST spend at least 1 hour on your own on just that one section that is hanging you up
- Both you AND your collaborator document your collaboration in your paper (once again, you are free to have fun with that, how would you document that in an actual paper?). I'm sorry, but "and then Lily helped me with that part" ain't exactly what I'd call "documented collaboration". Once again, imagine how an actual paper would actually CITE collaboration.... have some fun with that!
I will send a note home encouraging your folks at home to assist me in this regard...
Final Note: I'm basing this project on a favorite take-home test that we did in college for my Differential Equations (to be hip you gotta say "Diff E-Qs" class. It turned out to be a whole lot of fun (although we weren't allowed to collaborate); and most of us took Professor Lind at his word, and spent an hour or two every day working on it. It did NOT go well for folks who tried to do it all the night before)